Optimal design: Overview
Definition
A task falls into the category of optimal design when it involves the optimal choice of product parameters. In contrast to optimal control and optimal estimation, less emphasis is placed on time-varying systems and the estimation of unknown relationships.
Instead, the questions are less data-driven and more of a pre-analytical nature: Given concrete information about the goal of the design endeavor, which choice of parameters maximizes the success of the product equipped with such parameters?
Application areas
In such cases, the “product” can be a physical object as well as time-minimizing schedules, maximum efficiency experimental configurations, transport routes, resource allocations, or network designs. This list provides an incomplete overview.
The applications are enormously diverse and often have a direct business component. This is due to historical development reasons and the fact that time expenditure and costs are pressing and easy-to-interpret measures of success, whose minimization is of general interest. In its most general form
$$ \begin{align} \min_{x\in D} ~~~& f(x) \end{align}$$
optimal design includes optimizing uncertainties, stability and flexibility measures, physical as well as psychological metrics, and any other effects of the product. However, the more general the function, the less additional structure can be utilized to simplify the solution process.
Example
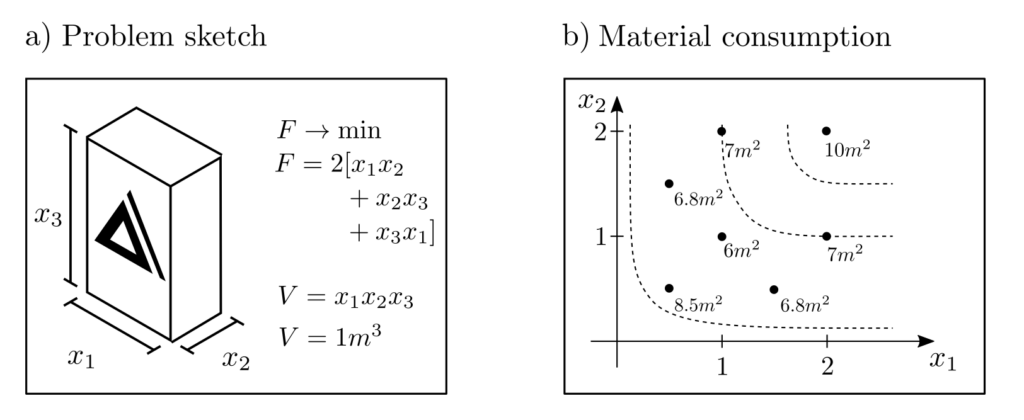
For a given volume \(V\) to be packaged in a box, the amount of packaging material required depends on the dimensions of the box’s sides. The optimization problem is then formulated as
$$ \begin{align} \min_{x_1, x_2, x_3} ~~~& F(x_1,x_2,x_3) \\ \text{s.t.} ~~~&x_1x_2x_3=V \end{align}$$
where \(F(x_1,x_2,x_3)=2[x_1x_2+x_2x_3+x_3x_1]\) represents the surface area of the box, thereby quantifying the consumption of packaging material. This problem can be easily solved by hand.
Given the constraint that \(x_1x_2x_3 = V\), our goal is to minimize the surface area. The minimal surface area for a given volume is achieved by a cube, as per the isoperimetric inequality in three dimensions. Thus, the solution to this optimization problem is a cube with sides of length \(\sqrt[3]{V}\), meaning \(x_1 = x_2 = x_3 = \sqrt[3]{V}\). This results in the minimal surface area and thus the minimal packaging material needed.
By excluding the nonsensical boundary cases where \(x_k=0\) for \(k=1, 2, 3\) and \(V=0\), the constraint can be transformed into the equation \(x_3 = (x_1x_2)^{-1}V\). The minimum is reached when \(\nabla F = 0\), i.e.,
$$\begin{bmatrix} \frac{\partial}{ \partial x_1} F \\ \frac{\partial}{\partial x_2} F \end{bmatrix} = \begin{bmatrix} 2 x_2 + \frac{V}{x_1^2} \\ 2x_1+ \frac{V}{x_2^2} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
This occurs precisely when \(x_1^2x_2 = x_2^2x_1 = V\), thus \(x_1 = x_2 = (x_1x_2)^{-1}V = x_3\). This directly implies \(x_1 = x_2 = x_3 = V^{1/3}\), meaning the optimal solution involves choosing a cubic packaging.
In reality, of course, further conditions must be considered: transportability, storability, and manufacturability of the packaging leading to size restrictions as well as the costs of the entire manufacturing process, not just the packaging material. This results in a geometric program whose solution is not as obvious.
Classes of problems
Surprisingly many practical tasks can be formulated as static design problems, including some with explicit time dependency. We will focus on problems for which reliable solution algorithms are available. This non-exhaustive overview of problem classes excludes some interesting nonlinear problems that do not fit the schema but can still be addressed with global optimization heuristics and manual tweaking.
Experiment design
Experimental design involves arranging individual experiments into a maximally effective combination. The goal may be the detectability of a specific parameter or the minimization of uncertainties in the statements that can be derived from the combination of experiments.
Constraints limit the resources available for the experiments or the simultaneity of the experiment execution. The products of this optimization are experiment combinations that minimize uncertainty.
Scheduling
Different machines perform various steps at different speeds, and a sequence of operations must be found such that all deadlines are met and the total processing time is minimized. Mathematically optimal scheduling is the big brother of ad-hoc planning with Gantt charts. The products of these optimizations are time-minimizing schedules.
Transportation and resource allocation
Nevertheless, there are algorithms that can reliably solve even more complicated transport problems involving various locations, goods, delivery capacities, and constraints. The products of these optimizations are cost-minimizing transport routes.
Topology- and network design
Networks and their topological properties play a significant role in the mathematical modeling of neighborhood relationships. They are important for representing matters concerning the flow of goods, forces, or logical connections.
Since networks often provide the formal framework for the constraints occurring in an optimization problem, their optimal design guarantees sensible behavior of the entities flowing within this network.
Practical aspects
Depending on the exact problem formulation and constraints, solving the aforementioned optimization problems can range from simple to impossible. Some transportation and scheduling plans can be formulated as linear programs and are therefore straightforward, while experimental design typically requires semidefinite programming, making it numerically challenging but still reliably solvable.
However, as soon as logical restrictions and discrete objects come into play, mixed-integer optimization must be employed. Then, no convergence guarantees can be made. Unfortunately, this is often the case when non-trivial constraints need to be considered. The vast amount of logistic literature is nevertheless a testament to the practical successes and the effectiveness of the approach.
Code
Example code: OD_product_packaging.py in our tutorialfolder