Optimal control: Robust optimal control

Problem statement

In robust opti­mal con­trol, the goal is to sta­bi­li­ze a sys­tem who­se exact dyna­mic pro­per­ties are unknown and can only be cons­trai­ned to a spe­ci­fic uncer­tain­ty ran­ge. Addi­tio­nal­ly, the sta­te of the sys­tem may only be par­ti­al­ly observable.

Trotz­dem soll ein zeit­ab­hän­gi­ger Input \(u(t)\) gefun­den wer­den, der den Sys­tem­zu­stand \(x(t)\) sta­bi­li­siert, d.h. \(\lim_{t\rightarrow \infty} x(t)=0\) unab­hän­gig von der eigent­li­chen Dyna­mik. Pro­ble­me die­ser Art tre­ten z.B. bei der Steue­rung von Droh­nen [1], Heli­ko­ptern, Fest­plat­ten­aus­le­se­al­go­rith­men [2] und gene­rell sobald die Steue­rungs­me­cha­nis­men eines Sys­tems Unsi­cher­hei­ten aufweisen.

Optimal control for uncertain dynamics

The dyna­mics of a sys­tem with par­ti­al­ly unknown dyna­mics are given by the equation

$$ \dot{x}(t) = Ax(t) + Bu(t) ~~~~~~[A,B] \in Co([A_1,B_1], …, [A_n,B_n]), $$

which cou­ples sys­tem chan­ges \(\dot{x}\) with the time-depen­dent sta­te varia­bles \(x(t)\) and con­trol inputs \(u(t)\). The matri­ces \(A\) and \(B\) are to repre­sent all pos­si­ble weigh­ted aver­a­ges \([\sum_{k=1}^n\lambda_k A_k, \sum_{k=1}^n \lambda_k B_k], \sum_{k=1}^n\lambda_k=1, \lambda_k \ge 0\) among the cor­ner points \([A_1, B_1], …, [A_n, B_n]\); this set is also cal­led the con­vex hull \(Co\). If \(A\) and \(B\) were known con­stant matri­ces, it would be a clas­sic plan­ning problem.

A sys­tem \(\dot{x}=Ax\) is sta­ble if the­re exists a qua­dra­tic func­tion \(V(x)=x^TPx, P\succeq 0\) such that [3, p. 428]

$$\dot{V}(x) = x^T(A^TP+PA)x <0.$$

This so-cal­led Lyapu­n­ov func­tion pro­ves that the­re is an ener­gy func­tion that explains all tra­jec­to­ries that can be gene­ra­ted by the sys­tem. A feed­back matrix \(K\) with \(u(t)=Kx(t)\) is sought, which sta­bi­li­zes the sys­tem. It can be deri­ved to \(K=YQ\) from the solu­ti­ons \(Q, Y\) of the fol­lo­wing semi­de­fi­ni­te sys­tem of equa­tions for the matri­ces \(Q\) and \(Y\) [3, p. 428].

$$ Q=Q^T \succ 0, ~~~~~~~~~ (QA_i^T+A_iQ)+(Y^TB_i^T+B_iY) \prec 0~~~~i=1, …,n$$

Example: Harmonic oscillator

The fol­lo­wing exam­p­le illus­tra­tes the appli­ca­ti­on and approach. A vibra­ting sys­tem is mass-pro­du­ced and used in dif­fe­rent situa­tions. Alt­hough the dyna­mics vary depen­ding on the situa­ti­on, a sin­gle, uni­ver­sal­ly valid feed­back con­trol for vibra­ti­on dam­ping is to be used.

Let \(s\) be the spa­ti­al varia­ble, and as usu­al, dot and dou­ble dot deno­te the first and second time deri­va­ti­ves, respec­tively. A har­mo­nic oscil­la­ti­on is cha­rac­te­ri­zed by the dif­fe­ren­ti­al equation

$$ \begin{align}\dot{s} & = — \omega s \\ x&=\begin{bmatrix} s \\ \dot{s} \end{bmatrix} \\ & \Rightarrow \dot{x}=\begin{bmatrix} \dot{s} \\ \ddot{s} \end{bmatrix} =\begin{bmatrix} \dot{s} \\ — \omega s \end{bmatrix}  = \begin{bmatrix} 0 & 1 \\ -\omega & 0 \end{bmatrix} \begin{bmatrix} s\\ \dot{s} \end{bmatrix}= Ax. \end{align}$$

Here, \(\omega >0 \) and the reso­nan­ce fre­quen­cy \(\sqrt{\omega}\) may vary depen­ding on the situa­ti­on. Sup­po­se \(\omega\) lies bet­ween \(1/2\) and \(3/2\) and the con­trol input is an acce­le­ra­ti­on; \(Bu=[0,0,u]^T\) with \(B=[0,0,1]^T\). Then the fol­lo­wing SDP needs to be solved.

$$ \begin{align} \min_{Q,Y} ~~~& \operatorname{tr} (Q) \\ \text{s.t.} ~~~&Q \succ 0 ~~~~ \operatorname{tr} Q \ge 1 \\ &(Q A_1^T +A_1Q)+(Y^TB^T + BY) \prec 0 \\ &(Q A_2^T +A_2Q)+(Y^TB^T + BY) \prec 0 \\ & A_1 =\begin{bmatrix} 0 & 1 \\ ‑1/2 & 0 \end{bmatrix} ~~~~~~~A_2=\begin{bmatrix} 0 & 1 \\ ‑3/2 & 0\end{bmatrix} \end{align}$$

This semi­de­fi­ni­te pro­gram can, for exam­p­le, be sol­ved with CVXPY [4] to \(K\approx [-60,-9]^T\). The effect of this feed­back matrix can be seen in the figu­re below.

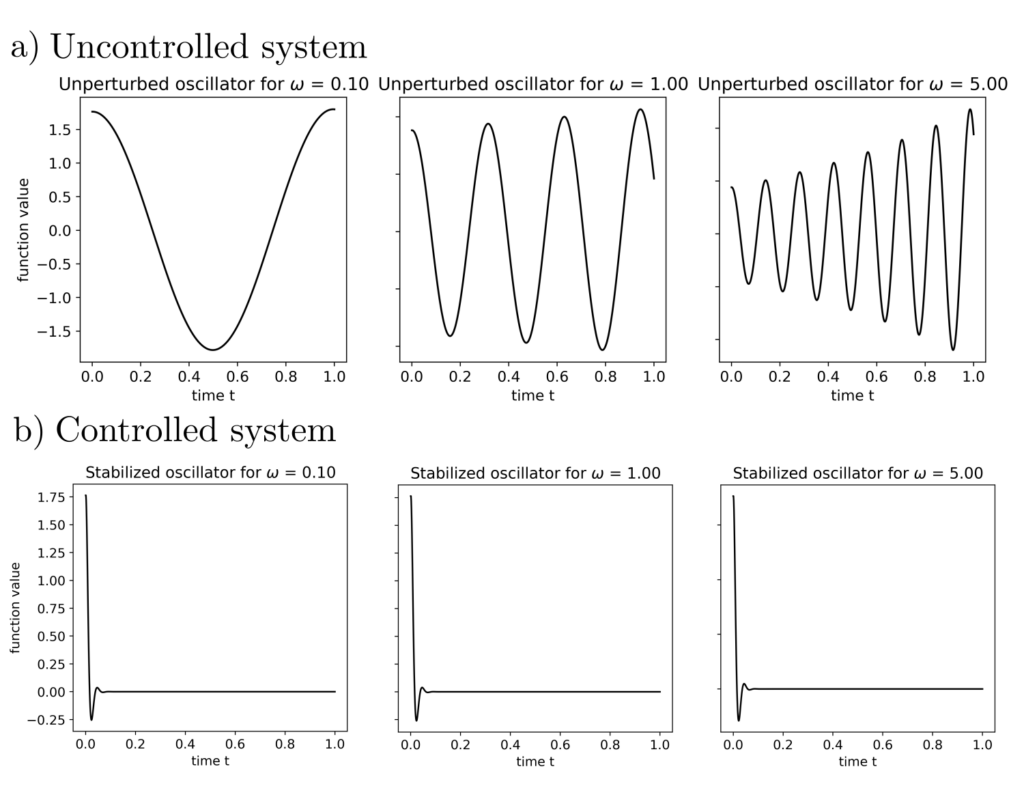
Figu­re 1: Dyna­mics of the har­mo­nic oscil­la­tor in the unin­fluen­ced sta­te (a) and with deve­lo­p­ment sta­bi­li­zed by the feed­back matrix \(K\) (b).

It is evi­dent that the abo­ve con­trol sta­bi­li­zes the sys­tems regard­less of the exact natu­ral fre­quen­ci­es. The tri­vi­al con­trol \(u=-s\), for exam­p­le, does not achie­ve this.

Unknown state and time-dependent dynamics

In a sys­tem to be con­trol­led, if the time-depen­dent sta­te \(x(t)\) can only be detec­ted through an out­put signal \(y(t)=C_yx(t)\), and the dynamics

$$ \dot{x}=A(t)x(t)+Bu(t) ~~~~~~~A(t) \in Co([A_1, …, A_n]) $$

are time-vary­ing, then the sys­tem is sta­bi­lizable only under cer­tain con­di­ti­ons. The matrix \(A(t)\) is a time-vary­ing line­ar com­bi­na­ti­on $$A(t)=\sum_{k=1}^n\theta_k(t)A_k ~~~~\sum_{k=1}^n \theta_k(t)=1, \theta_k(t)\ge 0.$$ It is an ele­ment of the con­vex hull \(Co([A_1, …, A_n])\), describ­ing the rela­ti­onship bet­ween sys­tem chan­ges \(\dot{x}\) and the sys­tem sta­te \(x\). The indi­rect­ly obser­ved sta­te \(x\) is to be stabilized.

Such pro­blems occur in sys­tems that need to be main­tai­ned sta­b­ly across a wide ran­ge of situa­tions and who­se descrip­ti­on includes non­line­ar terms and unob­ser­ved con­di­ti­ons [5]. This class of pro­blems includes the deve­lo­p­ment of auto­pi­lots for aero­space sys­tems and the opti­mal con­trol of che­mi­cal reac­tions in pro­cess engi­nee­ring [6].

SDP formulations

Assum­ing that the mixing coef­fi­ci­ents \(\theta_k(t)\) are known at any time, it can be shown that a sta­bi­lizable hig­her-dimen­sio­nal embed­ding of \(x\) exists if the semi­de­fi­ni­te sys­tem of equations

$$\begin{align} &\begin{bmatrix} S & I \\ I & R \end{bmatrix} \succeq 0 \\ &N_R^T(A_kR + R A_k^T)N_R \prec 0 ~~~~ k=1, …, n \\ &N_S^T(A_kS + S A_k^T)N_S \prec 0 ~~~~ k=1, …, n \end{align}$$

has a solu­ti­on \(S, R\) [3, pp. 428–431]. Here, \(N_R^T\) and \(N_S^T\) are matri­ces who­se colum­ns form the basis of the null spaces of \(B^T\) and \(C_y\), respec­tively. More details can be found in [7, pp. 22–23]. If the sys­tem of equa­tions is sol­va­ble, then the system

$$\begin{bmatrix} x \\ x_c \end{bmatrix} =\left( \underbrace{\begin{bmatrix} A(t) & 0 \\ I & 0\end{bmatrix}}_{\mathcal{G}} + \underbrace{\begin{bmatrix} 0 & B \\ I & 0 \end{bmatrix}}_{\mathcal{B}} \underbrace{\begin{bmatrix} A_c(t) & B_c(t) \\ C_c(t) & D_c(t) \end{bmatrix}}_{\Omega(t)} \underbrace{\begin{bmatrix} 0 & I \\C_y & 0 \end{bmatrix}}_{\mathcal{C}}\right) \begin{bmatrix}x \\ x_c \end{bmatrix}$$

can be sol­ved for the unknown clo­sed loop sta­te tran­si­ti­on matrix \(A_{cl}(t)=\mathcal{G}+\mathcal{B}\Omega(t) \mathcal{C}\). Fur­ther­mo­re, the con­di­ti­on \(A_{cl}^T(t)P+PA_{cl}(t) \prec 0 ~~~~~ P \succ 0 \)

can be satis­fied, ensu­ring the sys­tem is sta­ble sin­ce it dis­si­pa­tes ener­gy along all pos­si­ble tra­jec­to­ries. Sol­ving the sys­tem of equa­tions for each \(k=1, …, n\)

$$\begin{align}  &(\mathcal{G}_k+\mathcal{B}\Omega_k\mathcal{C})^TP + P(\mathcal{G}_K + \mathcal{B}\Omega_k \mathcal{C}) \prec 0 \\ &P=\begin{bmatrix} S & (S‑R^{-1})^{1/2} \\ (S_R^{-1})^{1/2 T} & I \end{bmatrix} ~~~~~~\mathcal{G}_K=\begin{bmatrix} A_k & 0 \\ 0 & 0 \end{bmatrix}\end{align}$$

for \(\Omega_k\) results in a time-depen­dent over­all solu­ti­on through a weigh­ted line­ar com­bi­na­ti­on of the indi­vi­du­al solu­ti­ons for \(\Omega_k\). The system

$$ \begin{bmatrix} \dot{X} \\ \dot{X}_c \end{bmatrix} = \left( \begin{bmatrix} \sum_{k=1}^n \theta_k(t) A_k & 0 \\ 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & B \\ I & 0 \end{bmatrix} \left(\sum_{k=1}^n \theta_k(t) \Omega_k \right) \begin{bmatrix} 0 & I \\ C_y & 0 \end{bmatrix}\right) \begin{bmatrix}x \\ x_c \end{bmatrix}$$

is sta­ble. The con­trol input \(u\) deri­ved from the out­put \(y\) is thus given by \(u(t)\) with

$$\begin{align} u(t) &= \sum_{k=1}^n \theta_k(t) C_c^kx_c + \sum_{k=1}^n \theta_k(t) D_c^ky \\ \Omega_k&=\begin{bmatrix} A_c^k & B_c^k \\ C_c^k & D_c^k\end{bmatrix} \end{align}$$

whe­re \(x_c\) evol­ves accor­ding to \(\dot{x}_c = \sum_{k=1}^n A_c^kx_c+\sum_{k=1}^n\theta_k(t) B_c^kC_yx\).

Example: Circuit

An exam­p­le illus­tra­tes the approach. Con­sider a cir­cuit with a resis­tor, an induc­tor, and a capa­ci­tor. Accor­ding to [8, pp. 10–11], the rela­ti­onship bet­ween vol­ta­ge \(V\), cur­rent \(I\), and time \(t\) is given by the vec­tor-valued dif­fe­ren­ti­al equation

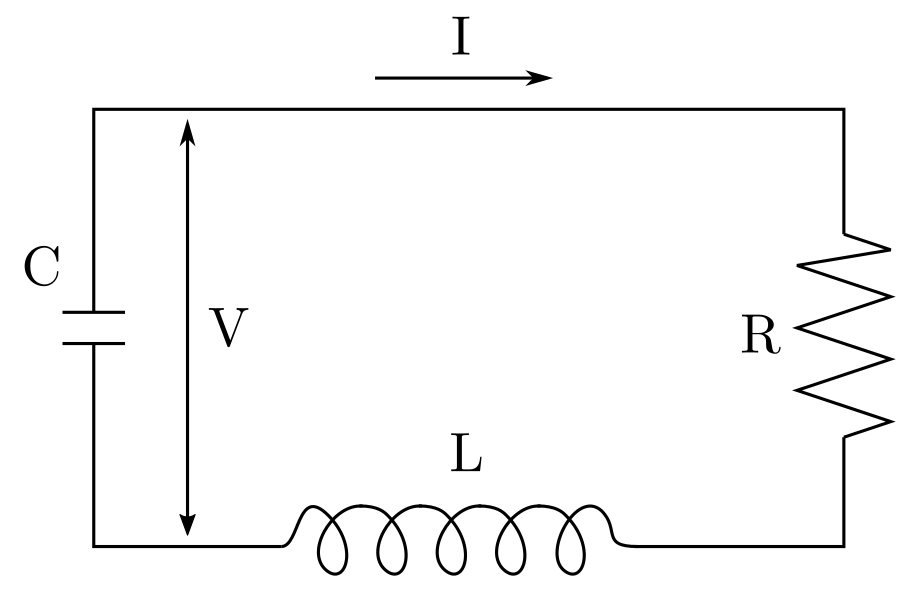
$$ \begin{bmatrix} \dot{V} \\ \dot{I}\end{bmatrix}  = \begin{bmatrix}0 & — 1/C \\ 1/L & ‑R/L\end{bmatrix} \begin{bmatrix} V\\ I \end{bmatrix} + \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} $$

whe­re \(R\) is the resis­tance, \(L\) is the induc­tance of the coil, and \(C\) is the capa­ci­tance of the capa­ci­tor. We assu­me that:

  1. The chan­ge in vol­ta­ge and cur­rent can be con­trol­led via the con­trol input \([u_1,u_2]^T\).
  2. \(C\) and \(L\) vary bet­ween 1 and 10.
  3. Only the cur­rent is obser­va­ble, and the vol­ta­ge is not measured.

Despi­te the pro­ble­ma­tic con­di­ti­ons 2. (varia­ble cir­cuit para­me­ters) and 3. (vol­ta­ge not obser­va­ble), the sys­tem is to be sta­bi­li­zed. We app­ly the equa­tions pre­sen­ted abo­ve and obtain the fol­lo­wing chain of semi­de­fi­ni­te sys­tems of equa­tions, which we can sol­ve, for exam­p­le, with CVXPY.

$$\begin{align}1.~~~~ \text{find} & ~~~R, S \\ s.t. &~~~ \begin{bmatrix} R & I \\ I &S \end{bmatrix} \succeq 0 \\ &~~~ \begin{bmatrix} 1 & 0\end{bmatrix} (S A_k + A_k^TS) \begin{bmatrix} 1 \\ 0 \end{bmatrix} <0 ~~~~~~k=1, …, 4 \\ &~~~ A_1=\begin{bmatrix} 0 & ‑1 \\ 1 & ‑R\end{bmatrix} ~~~~~A_2=\begin{bmatrix} 0 & ‑0.1 \\ 1 & ‑R\end{bmatrix} \\ & ~~~A_3=\begin{bmatrix} 0 & ‑1 \\ 0.1 & ‑0.1R\end{bmatrix}~~~~~A_4=\begin{bmatrix} 0 & ‑0.1 \\ 0.1 & ‑0.1R\end{bmatrix}\\2.~~~~ \text{find} & ~~~\Omega_k \\ s.t. &~~~(\mathcal{G}_k + \mathcal{B}\Omega_k \mathcal{C})^TP+P(\mathcal{G}_k+\mathcal{B}\Omega_k\mathcal{C}) \prec0 \\ & ~~~\mathcal{G}_k= \begin{bmatrix} A_k & 0 \\ 0 & 0\end{bmatrix} ~~~~~\mathcal{B}=\begin{bmatrix} 0& 0& 1&0\\0&0&0&1\\1&0&0&0\\0&1&0&0\end{bmatrix} ~~~~~\mathcal{C}=\begin{bmatrix} 0&0&1&0\\ 0&0&0&1\\ 0&1&0&0\end{bmatrix} \end{align}$$

The result is visi­ble in the figu­re below.

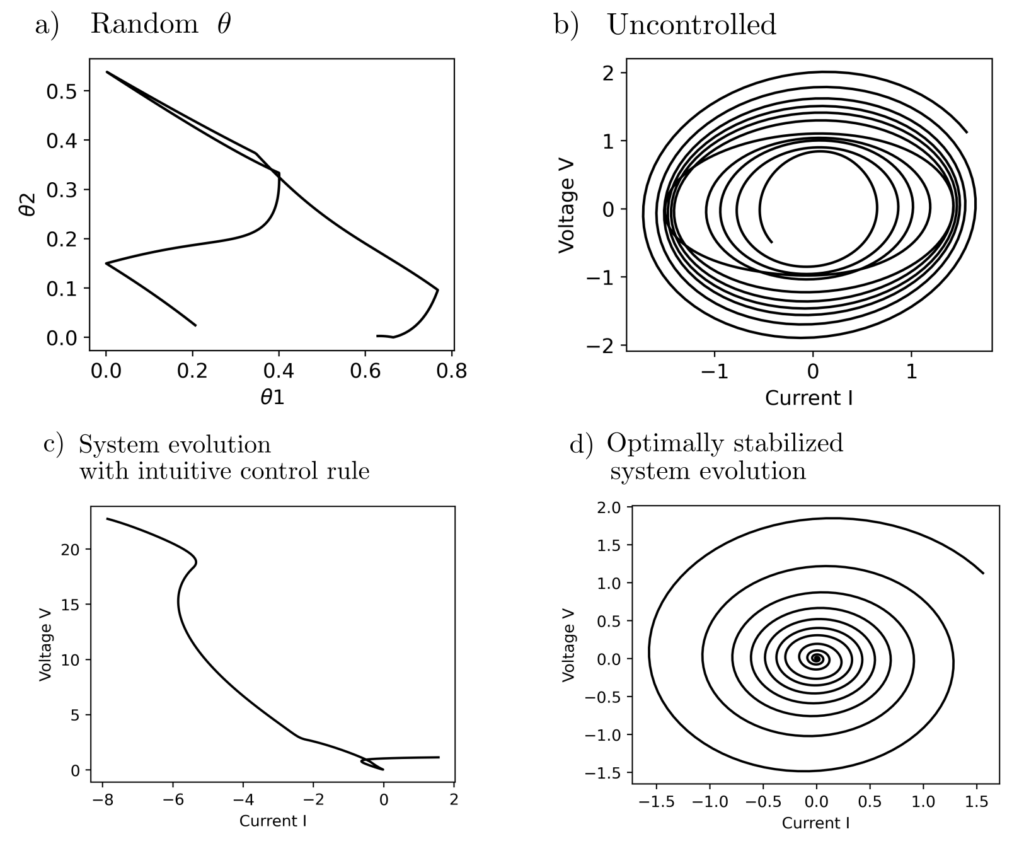
Figu­re 2: Sys­tem evo­lu­ti­on for ran­dom \(\theta\) (a), when the con­trol input is set to \(u=0\) (b), cho­sen inver­se­ly pro­por­tio­nal to the cur­rent ©, or deter­mi­ned via the SDP sys­tem of equa­tions (d).

Inde­ed, the sys­tem is sta­ble. This is not the case if the con­trol input is cho­sen accor­ding to intui­ti­ve, manu­al­ly con­cei­ved rules or left to its­elf. The­r­e­fo­re, the approach to opti­mal con­trol of only par­ti­al­ly obser­ved sys­tems with par­ti­al­ly unknown dyna­mics pro­vi­des real added value.

Code & Sources

Exam­p­le code: OC_harmonic_oscillator_3.py , OC_harmonic_oscillator_4.py  in our tuto­ri­al­fol­der.

[1] AlS­wai­lem, S.I. (2004). Appli­ca­ti­on of Robust Con­trol in Unman­ned Vehic­le Flight Con­trol Sys­tem Design. Dis­ser­ta­ti­on Cran­field Uni­ver­si­ty, Cranfield.

[2] Post­le­thwai­te, I., Tur­ner, M. C., Gui­do, H. (2007). Robust Con­trol Appli­ca­ti­ons. Annu­al Reviews in Con­trol, 31, (1), 27–39

[3] Wol­ko­wicz, H., Sai­gal, R., & Van­den­berg­he, L. (2012). Hand­book of Semi­de­fi­ni­te Pro­gramming: Theo­ry, Algo­rith­ms, and Appli­ca­ti­ons. Ber­lin Hei­del­berg: Sprin­ger Sci­ence & Busi­ness Media.

[4] Dia­mond S., & Boyd S., (2016). CVXPY: A Python-embedded mode­ling lan­guage for con­vex optimi­zation. Jour­nal of Machi­ne Lear­ning Rese­arch, 17(83), 1–5.

[5] Leith, D. J., & Lei­t­head, W. E. (1998). Appro­pria­te rea­li­sa­ti­on of MIMO gain-sche­du­led con­trol­lers. Inter­na­tio­nal Jour­nal of Con­trol, 70, (1), 13–50.

[6] Klatt, K. U., & Engel S. (1998). Gain-sche­du­ling tra­jec­to­ry con­trol of a con­ti­nuous stir­red tank reac­tor. Com­pu­ters & Che­mi­cal Engi­nee­ring, 22, 491–502.

[7]  Boyd, S., El Ghaoui, L., Feron, E., & Bal­a­krish­n­an, V. (1994). Line­ar Matrix Ine­qua­li­ties in Sys­tems and Con­trol Theo­ry. Phil­adel­phia: SIAM Stu­dies in Appli­ed and Nume­ri­cal Mathematics.

[8] Schein­erman, E. R. (2013). Invi­ta­ti­on to Dyna­mi­cal Sys­tems. New York: Cou­rier Corporation.