Courses and tutorials - Atlas optimization

Offerings: Courses

Overview

We offer several half-day and full-day courses. They are aimed at generally interested individuals without prior experience (Optimization I, Machine Learning I) and at those who regularly deal with mathematical modeling and wish to deepen their skills.

In the advanced courses, material from the areas of optimal estimation, optimal control, and deep learning is covered. They provide the tools needed to solve concrete real-world problems.

Format

We place importance on a healthy mix of theory and practice. Application-oriented tutorials using freely available state-of-the-art open-source software are part of the program, as are informal discussions, presentations of fundamental theory, practical examples, new insights, or the derivation of equations. The exact mix of these different elements is determined by the course objectives and to a large extent by the participants.

Your personal benefit is important to us. In the courses,

we present everything necessary on the topics of optimization and machine learning,
you will discuss and implement practical examples on laptops provided by us,
you will get to know functioning software and take it home.

You will be supervised by a competent staff member, who will support you during the learning experience and help you convert the theoretical knowledge into practical gains usable for your projects.

Courses

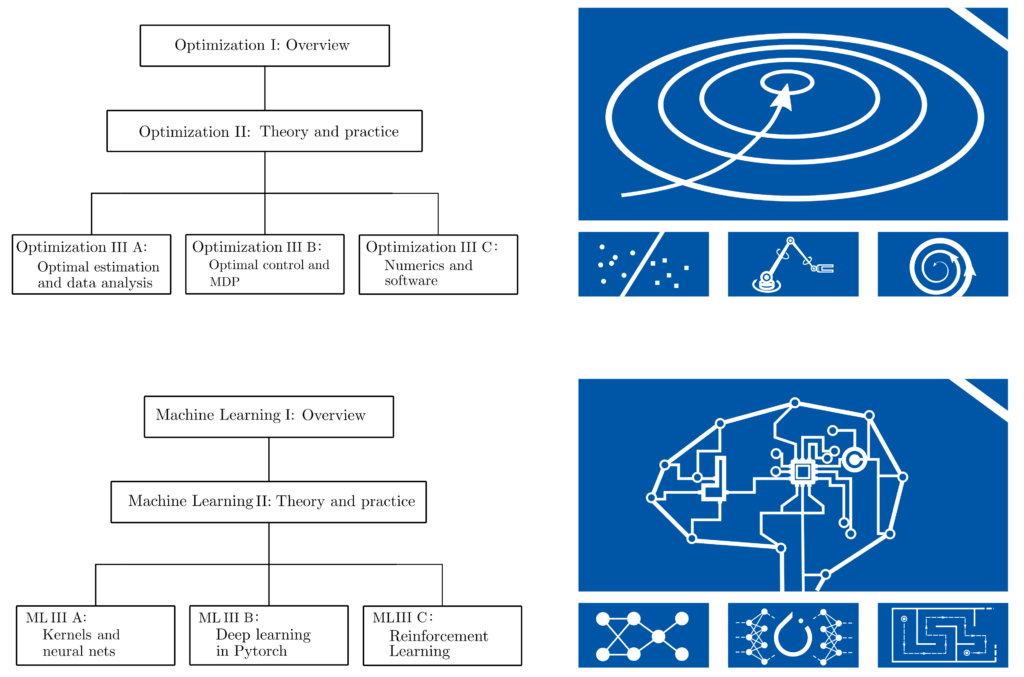
Detailed explanation

Basic information about the theories and applications of optimization and machine learning can be found here and here. Have we piqued your interest or do you need more information? Then contact us and share your questions or suggestions. Participation in the courses is possible from Fall 2024; registration will then be open.

Course	Duration	Topics
Optimization I: Overview	2 h	Definition of Optimization, Practical Relevance of Optimization Problems, Examples from Nature, Technology, Economy, Solvability of Optimization Problems, State of the Art Research Directions, Practical Aspects
Optimization II: Theory and practice	4 h	Mathematical formulation of optimization problems, linear, quadratic, second order cone, semidefinite, stochastic, and dynamic programming, areas of application, example problems, modeling techniques, Python and CVXPY.
Optimization III A: Optimal estimation and data analysis	6 h	Stochastic models, least squares, parameter estimation, interpolation and smoothing of high-dimensional data, Hilbert spaces, Gaussian process regression, indirect observations, worst-case probability estimates.
Optimization III B: Optimal control and Markov decision processes	6 h	System analysis, system identification, stability, controllability and observability, linear quadratic controllers, robust optimal control, stochastic optimal control, linear matrix inequalities and semidefinite programming, Markov decision processes, state of the art, example applications.
Optimization III C: Numerics and software	4 h	Naive methods, convexity, Newton’s method, interior point methods, duality, standard formulations, programming LP and QP solvers yourself, CVXPY, formulating problems in CVXPY, interpretation of outputs, state-of-the-art open source and commercial solvers.
ML I: Overview	2 h	Definition and differentiation of machine learning, overview, success stories, supervised learning, unsupervised learning, reinforcement learning, application examples, failure cases, optimization formulations and solutions, what can be solved with ML?
ML II: Theory and practice	4 h	ML as a statistical optimization problem, simple examples, the classic five tasks, examples and Python libraries, neural networks, training and testing, architecture of ML software and packages.
ML III A: Kernels and neural Nets	6 h	Infinite-dimensional spaces and kernels, features and feature design, nonlinear features, support vector machines, RKHS and the kernel trick, ANNs as universal function approximators, architecture and training, convergence, interpretations of layers, applications such as neural style transfer.
ML III B: Deep learning with PyTorch	6 h	Manual features vs deep learning, learning from images, network architecture, recognition of postal codes in images, SVMs vs DL, non-convexity, convergence problems, ADAM, practical implementation in PyTorch, insights into an ANN, ImageNet, network architectures for text, image, and time series data.
ML III C: Reinforcement learning	6 h	Limits of classical optimal control formulations, reward formalism, reinforcement learning paradigms, biological foundations, Markov decision processes, policies as solutions, stochastic transition models, exploration vs. exploitation, current successes and algorithms, implementation in Stable Baselines3, example applications.

Programming language

In the courses, we use the Python programming language and the open source frameworks CVXOPT, CVXPY, PyTorch, Pyro, and Stable Baselines3 as well as our custom-designed Atlas Optimization Suite. Optimization and machine learning problems can be formulated and solved using these software packages through a graphical user interface, without the need to delve into programming details.

The advanced courses are thus also suitable for individuals without programming knowledge. However, some experience with mathematical methods is required. The courses take place in Zurich or, upon company request, externally.