Overview: Mathematical optimization

Definition
Mathematical optimization is the science of making the best possible decision. It lies at the intersection of mathematics, software, and industrial application and has seen tremendous growth over the last few decades due to its practical relevance and continuous computational advances. It has become one of the most current and practically relevant fields of modern applied mathematics and is indispensable in many industrial sectors.
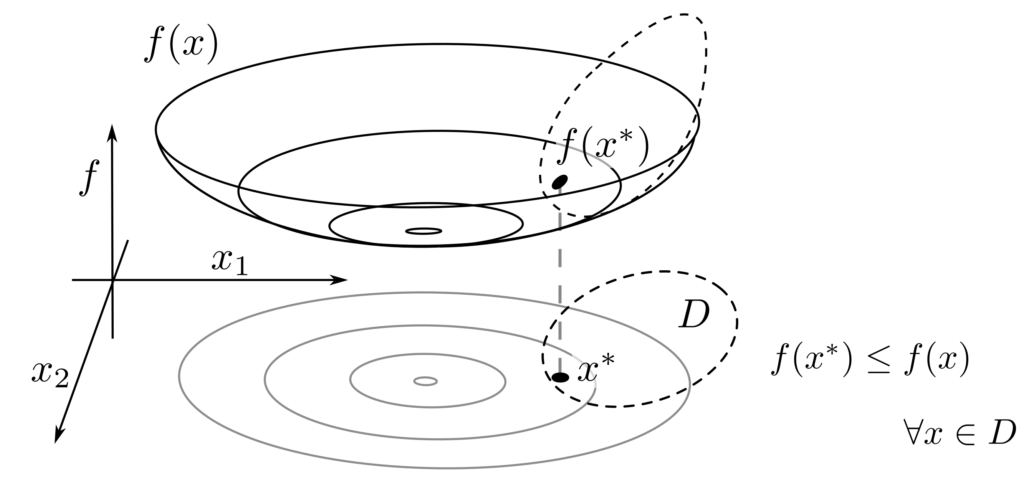
Mathematical optimization deals with optimization problems, i.e., tasks of the form:
\[
\begin{align}
\min_{x} ~~&f(x) \\
\text{s.t.} ~~& x \in D
\end{align}
\]
This is to be understood as the search for a choice of the vector \(x\) such that the function \(f(x)\) achieves the smallest value while \(x\) meets certain properties \(D\).
Explanation
The function \(f(x)\) is called the objective function and represents the quantity whose value is to be minimized. This could include costs, time durations, or risks. The vector \(x\) contains the decision variables — control variables, whose values can be chosen to influence the objective function. The constraint \(x \in D\) defines restrictions to which the decision variable is subject. For example, if \(x\) were a quantity of material, then the requirement \(x \geq 0\) might be sensible.
Relevance
When the three components—objective function, decision variables, and constraints—are carefully selected and combined to represent a real-world problem, the solution to the optimization problem yields the best possible course of action. Therefore, optimization is a very powerful tool when decisions need to be made that have far-reaching and complex consequences. The specific applications may involve selecting product parameters, designing schedules, estimating unknown quantities, or setting control signals.
Especially in complex real-world problems, this often leads to mathematical models with thousands of decision variables and constraints. Solving such models has only become possible through the explosive growth in computing power of modern computers and the development of dedicated optimization software. A unified theory for the study of optimization problems has since been developed, leading to a set of methods that have often been profitably applied in practice.
Theory
Optimization problems come in all shapes and colors and can cover all complexity criteria from simple to impossible. Objective functions of optimization problems can be studied and classified based on their mathematical properties. For example, if they are convex, guarantees can be made about the unique solvability of the problem.
It is often also possible to find lower bounds for the minima, thus proving the optimality of a proposed solution. These relationships are used by numerical methods that iteratively set up and solve systems of equations until no further improvements are possible.
Methods
Depending on the characteristics of the optimization problem, there may be tailor-made methods for its solution. This primarily involves distinguishing based on the degree of nonlinearity in the optimization problem and the role of randomness. Optimization problems with a linear objective function and linear constraints are known as Linear Programs.
They can be reliably solved, even when the number of decision variables reaches into the hundreds of thousands. Nonlinear components of a problem must take certain forms to not jeopardize solvability. The same applies when random effects need to be considered. Either the probabilistic requirements are transformed into (nonlinear) conditions, or stochastic simulations must be employed. Developing highly specialized and powerful algorithms is challenging in any case. Fortunately, there is now freely available and open-source software.
Applications
The practical applications are diverse and hard to oversee. Making optimal decisions as an abstract goal is so general that virtually any real-world problem can be formulated as optimization problems. Of course, this does not necessarily mean that they are solvable. Practical applicability of optimization methods to industrial problems requires careful formulation of objectives and constraints and sometimes specialized solution algorithms.
This requires investement into research; an effort that is still being undertaken. The greatest successes in optimization have been achieved in areas such as finding optimal schedules, traffic routes, resource distributions, stock portfolios, model parameter sets, probability distributions, estimators, system controls, and maximally stable game strategies. We divide this heterogeneous set of applications into the disciplines of optimal design, optimal estimation, and optimal control.
Context
The transitions and intersections with machine learning are numerous. Since typically every machine learning problem can be written as the optimization of success probabilities, optimization is an integral aspect of data-driven learning. Mathematical optimization is versatile, practical, and powerful. It is no exaggeration to call it one of the most promising disciplines of modern applied mathematics.