Overview: Machine learning
General
On the following subpages, you will find information about the types of problems that can be solved using Machine Learning (ML). The methods used and the basic theory are briefly outlined; code examples detail practical applications.
Relevance
Definition
Unlike mathematical optimization, the task of machine learning (ML) is less clearly defined—it does not just involve solving an equation. Instead, ML deals with the development and analysis of algorithms whose performance improves with increasing amounts of data. Mathematically, this can be formalized as the minimization of a loss function \(f_S(x)\) under constraints \(D\) for the parameters \(x\), the determination of which is the goal of learning.
$$ \begin{align} \min_x ~~~&f_S(x) \\ \text{subject to} ~~~&x \in D \end{align}$$
However, compared to classical optimization, \(f_S(x)\) is an a priori unknown function that only takes shape through real-world data \(S\). For example, for an ML program learning to play chess, it is only clear which game situations are desirable after it has played several rounds and evaluated the experience from these rounds. The combination of data-dependent models and mathematical optimization is typical for ML.
Context
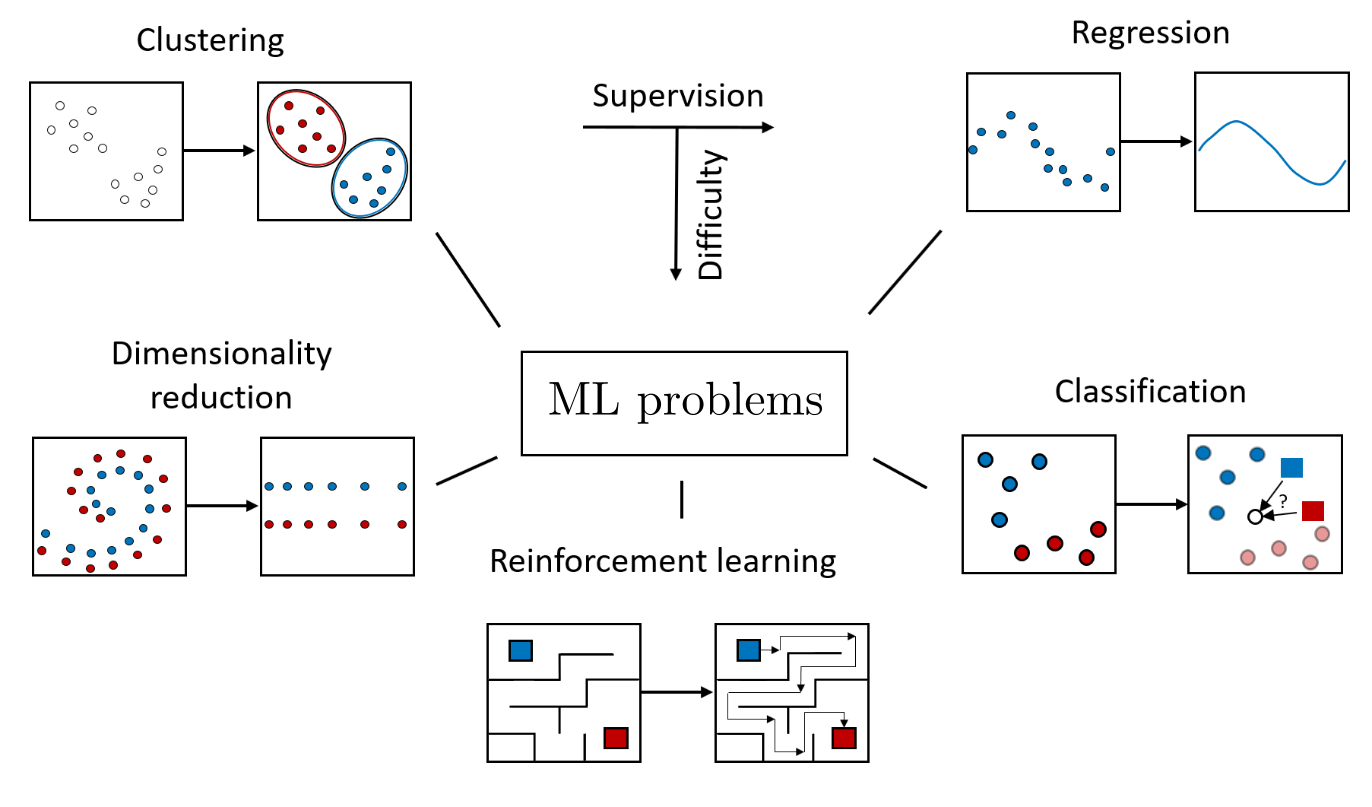
In this respect, ML algorithms differ from classical software, which is a closed system consisting of a fixed sequence of commands and thus is not capable of altering its own functionality by integrating new data. The ability to learn from new experiences, along with the ubiquity of certain types of data, makes ML flexible and versatile, but also complex in its overall array of methods. Typically, ML is divided into three classes of tasks: supervised learning, reinforcement learning, and unsupervised learning. The following image provides a rough overview.
Examples
Depending on which loss function \(f_S(x)\) is chosen, an algorithm can be directed to solve various tasks: \(f_S(x)\) can measure prediction errors, misclassification rates, penalties for suboptimal system controls, intra-group variances, or reconstruction errors. Optimally chosen parameters \(x_1, x_2, …\), determine the behavior of the algorithm such that the loss function (as a measure of the impact of undesirable behavior) takes on the smallest possible values. Different meanings of \(f_S(x)\) and associated applications are noted in the table below.
| Example | \(f_S(x)\) | \(S\) | \(V(x_1,x_2,…)\) |
|---|---|---|---|
| Price prediction | Prediction error | Product features, prices | Price |
| Machine translation | - Sentence probability | Pairs of sentences | Translated sentence |
| Image classification | Misclassification rate | Images object classes | Class probabilities |
| Cancer diagnosis | Misclassification rate | Medical data, diagnoses | Cancer probability |
| Machine control | Ineffective system dynamics | Previous control cycles | Control signals |
| Game AI | Probability of defeat | Previous games | Game strategy |
| Data compression | Reconstruction error | Example data | Compressed object |
| Fraud identification | Behavioural consistency | Metadata transactions | Irregularity transaction |
Applications
Many practical tasks from disciplines such as finance, marketing, medicine, image processing, game theory, data analysis, etc., can be formulated as an ML problem \(\min_x f_S(x), x \in D\). Regardless of the specific application, we identify three classes of tasks into which tasks from the above disciplines can be categorized:
Supervised learning
Supervised learning refers to ML tasks where the desired behavior of the algorithm can be directly specified in the form of data, particularly through regression and classification. A model (e.g., a neural network) should then be adjusted in terms of its parameters so that the model behavior represents the exemplary data as accurately as possible. If the model is well-chosen, it not only replicates input-output relationships set by the data but also acts plausibly in new situations not covered by the training data. This class of tasks includes creating statistical models, predictive analytics, classification of text, audio, images, videos, text translation, automatic generation of subtitles, and much more.
Reinforcement Learning
Reinforcement learning refers to ML tasks where there is positive and negative feedback to assess the behavior exhibited by the algorithm, but there are no direct hints on which behavior is exemplary and therefore to be imitated. The algorithm interacts with a system that it can modify with control signals, upon which the system responds with a change and reinforcing or punitive feedback. Reinforcement learning thus mimics the learning behavior in real and uncertain contexts, similar to a person playing chess for the first time. The goal is to derive optimal sequences of decisions under uncertainty and in competitive situations. This class of tasks includes optimal machine control, training AIs in games, active portfolio management, traffic flow management, warehouse management, and procurement planning.
Unsupervised learning
Unsupervised learning involves the algorithm receiving no immediate guidelines on the desired behavior. The algorithm must independently discover patterns in the data without prior learning experience. These patterns are then used to cluster the data or reduce it to its most important components. This process generates a structure on a dataset that can subsequently be used to, for example, identify atypical financial transactions, cluster related genes, identify ecologically connected plant communities, operate recommender systems, segment markets into groups, or analyze social networks.

Outlook
The aforementioned tasks are standard machine learning (ML) tasks with specially designed algorithms that have been successfully tested in practice. We present some example problems below and illustrate their solutions with code, sketches, and descriptions. We emphasize explaining the relationship between the behavior of an ML algorithm, the loss functions, and the real-world implications. Ultimately, we formalize these as optimization problems again. Compared to formulations in classical mathematical optimization, however, data-driven nonlinear terms such as cross-entropy, Kullback-Leibler divergences, and parameters in neural networks appear, which do not allow for reliable optimization. This leads to experimental numerical methods; however, for neural networks, there is still good publicly available software such as PyTorch.
Practical applications, methods, and theory can be found in the sections named accordingly. We hope the material inspires you in identifying or searching for applications of machine learning in your business.