Mathematical Optimization: Methods
Numerical analysis
If an optimization problem \( \min f(x), x \in D\) is formulated, it still needs to be solved. The exact process of solving it depends on the structure of the function \( f(x) \) and the search space \( D\). If both are nonlinear, the problem may not be solvable with current methods. In any case, solving optimization problems falls within the domain of numerical analysis—the branch of mathematics that deals with the construction of algorithms to solve mathematical problems.
The development of numerical algorithms is a challenging task that requires trade-offs regarding rounding errors, computational intensity, memory requirements, runtime, correctness, and reliability of the solution proposed by the algorithm. Typically, such an algorithm processes the problem data \(f\) and \(D\) according to a nonlinear and iterative scheme, which has significant potential for errors.
Classes of optimization problems
Fortunately, for certain archetypal classes of functions \(f\) and search spaces \(D\), reliable solution algorithms have already been developed and implemented as computer programs. Consequently, an optimization problem is most comfortably solved when it can be reformulated as an instance of a class of optimization problems for which solution algorithms are available. These include the following configurations.
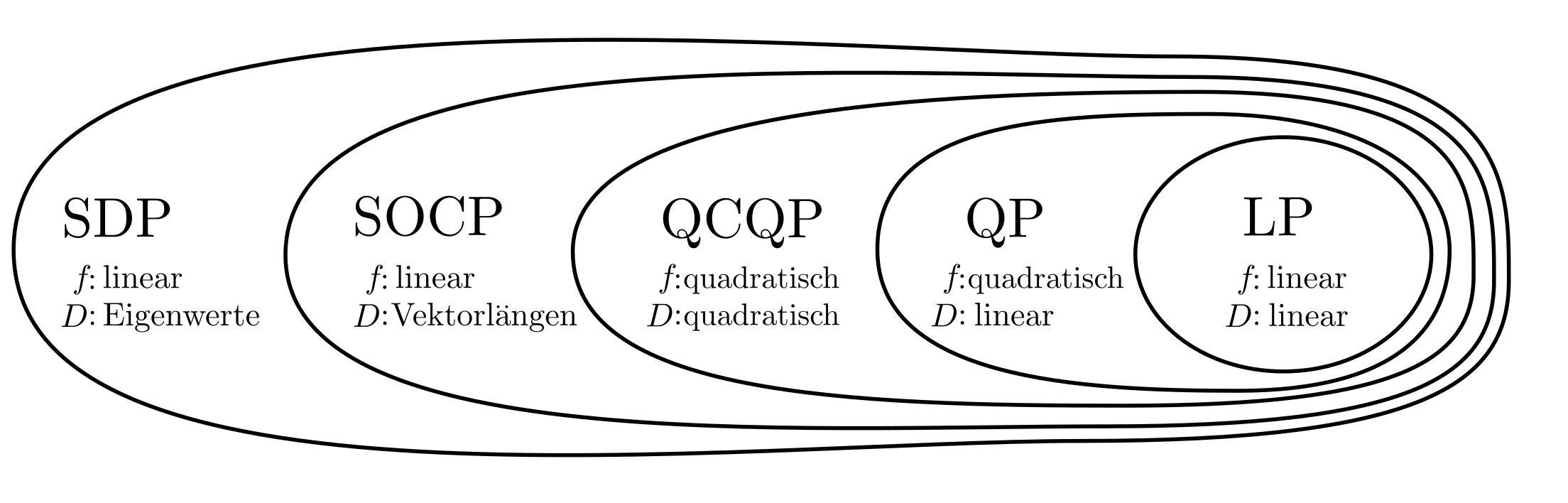
Relationship between the classes
If the optimization problem
$$ \begin{align} \min_x ~~~&f(x) \\ \text{s.t.} ~~~&x \in D \end{align}$$
can be formulated as an LP, QP, QCQP, SOCP, or SDP, thus involving certain second-order polynomials, then it can be reliably solved with limited computational effort. Other problem classes exist, such as Geometric Programming [1, p. 160], log-log convex Programming [2], or Maxdet Problem [3], but the aforementioned classes already cover a wide spectrum.
Additionally, dynamic programming, which deals with the optimization of sequences of decisions, is of great practical importance in operational optimization. For many of the above classes, the further constraint \( x \in Z\) can also be added, i.e., \(x\) should be integral. Considering such conditions can be sensible when \(x\) represents discrete indivisible units like logical yes-no decisions. However, the solution algorithms become considerably less reliable, and no guarantees can be offered. The problem is non-convex and NP-hard just like the so-called black-box optimization for functions without known structure.
Outlook
On the subordinate pages, you will find information about LP, QP, QCQP, SOCP, SDP, and their mixed-integer variants, as well as about dynamic programming and black-box optimization.
Sources
[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[2] Agrawal, A., Diamond, S., & Boyd, S. (2019). Disciplined geometric programming. Optimization Letters, 13(5), 961–976.
[3] Vandenberghe, L., Boyd, S., & Wu, S. (1998). Determinant Maximization with Linear Matrix Inequality Constraints. SIAM Journal on Matrix Analysis and Applications 1998 19:2, 499–533
